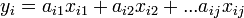Aritalab:Lecture/JSBi/Test/Math
From Metabolomics.JP
< Aritalab:Lecture | JSBi/Test(Difference between revisions)
(New page: =確率・統計= ===分散と共分散・相関=== 分散とは一つのデータ集合におけるばらつきの度合いであり、共分散は二組の対応するデータ間がば...) |
m |
||
| (11 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | = | + | =確率= |
| − | === | + | * [[Aritalab:Lecture/Basic/Expectation|期待値と分散について]] |
| − | + | ||
| − | + | =分布= | |
| − | + | * [[Aritalab:Lecture/Basic/Distribution|分布について]] | |
| − | + | ||
| − | + | =統計・推定= | |
| − | + | 母集団から無作為に抽出された標本集団から、もとの母集団を統計的に推し量ることを推定という。 | |
| − | :<math> | + | ===回帰分析=== |
| + | 従属変数(近似したい値、目的変数ともいう)と説明変数(近似に用いるデータ)の関係を統計的に推定することを回帰分析という。 | ||
| + | 1個の説明変数から1個の従属変数を予測する場合を単回帰、説明変数を複数用いる場合を重回帰という。 | ||
| + | 従属変数を<i>y</i>、説明変数を<i>x</i>とすると | ||
| + | :<math> y_i = a_{i1}x_{i1} + a_{i2}x_{i2} + ... a_{ij}x_{ij}</math> | ||
| + | の形でパラメータ<i>a_{ij}</i>を最小二乗法で決定する線形回帰が一般的。 | ||
| + | |||
| + | ==点推定と区間推定== | ||
| + | 標本の値から、母集団の平均値や分散を予測することを点推定(数値を点として予測)と呼び、その推定がどれ位ずれているかを区間推定と呼ぶ。 | ||
Latest revision as of 15:35, 24 May 2011
Contents |
[edit] 確率
[edit] 分布
[edit] 統計・推定
母集団から無作為に抽出された標本集団から、もとの母集団を統計的に推し量ることを推定という。
[edit] 回帰分析
従属変数(近似したい値、目的変数ともいう)と説明変数(近似に用いるデータ)の関係を統計的に推定することを回帰分析という。 1個の説明変数から1個の従属変数を予測する場合を単回帰、説明変数を複数用いる場合を重回帰という。 従属変数をy、説明変数をxとすると
の形でパラメータa_{ij}を最小二乗法で決定する線形回帰が一般的。
[edit] 点推定と区間推定
標本の値から、母集団の平均値や分散を予測することを点推定(数値を点として予測)と呼び、その推定がどれ位ずれているかを区間推定と呼ぶ。