Aritalab:Lecture/NetworkBiology/Markov Chains/Birth-death Process
m (New page: ==出生死亡過程== ===モラン過程=== 個体数を ''n'' とし、状態 ''i'' から ''i''+1, ''i''-1 の状態へそれぞれ確率<math>\alpha, \beta \ (\alpha + \beta < 1)</math...) |
m |
||
| Line 29: | Line 29: | ||
<math>\textstyle y_{i+1} = \gamma y_i, \quad \sum^n_{i=1} y_i = 1</math> | <math>\textstyle y_{i+1} = \gamma y_i, \quad \sum^n_{i=1} y_i = 1</math> | ||
| − | + | を得る。Moran過程では通常、少ない個体数から''n''個体にまで増殖するケースを考えるため、<math>\gamma</math>は1より小さい値と考えてよい。 | |
<math> y_1 = x_1, \ y_2 = \gamma x_1, \ y_3 = \gamma^2 x_1, \cdots, y_n = \gamma^{n-1} x_1 </math> | <math> y_1 = x_1, \ y_2 = \gamma x_1, \ y_3 = \gamma^2 x_1, \cdots, y_n = \gamma^{n-1} x_1 </math> | ||
| Line 57: | Line 57: | ||
</math> | </math> | ||
| + | ===式の解釈=== | ||
''n'' 個体の集団において、全ての個体が最初タイプAであるとする。 | ''n'' 個体の集団において、全ての個体が最初タイプAであるとする。 | ||
このときタイプBという突然変異が1個生じたとする。 | このときタイプBという突然変異が1個生じたとする。 | ||
| − | タイプBが <math>\gamma < 1</math>を満たす、すなわち<math>\alpha</math>が<math>\beta</math> | + | タイプBが <math>\gamma < 1</math>を満たす、すなわち<math>\alpha</math>が<math>\beta</math>よりも大きくて個体数を増やす傾向にあると仮定する。 |
| + | タイプBが何らかの優性種であると考えてもよい。 | ||
初めに1個生じたタイプBが集団 ''n'' の中に固定される(集団全体をカバーする)確率は<math>x_1 \xrightarrow{n \rightarrow \infty} 1 - \gamma</math>。 | 初めに1個生じたタイプBが集団 ''n'' の中に固定される(集団全体をカバーする)確率は<math>x_1 \xrightarrow{n \rightarrow \infty} 1 - \gamma</math>。 | ||
つまり、Aより10倍優位な変異体であっても (<math>\gamma = 1/10</math>)、集団全体にその変異が保持される確率は 9/10 でしかない。 | つまり、Aより10倍優位な変異体であっても (<math>\gamma = 1/10</math>)、集団全体にその変異が保持される確率は 9/10 でしかない。 | ||
| + | 通常の遺伝子変異で生存戦略に極めて優性となるケースは非常に稀だとすれば、殆どの変異は集団全体に保持されないことになる。 | ||
===木村の中立進化説=== | ===木村の中立進化説=== | ||
突然変異が完全に中立な場合、<math>\gamma = 1</math> から <math>x_1 = 1/n</math>となる。 | 突然変異が完全に中立な場合、<math>\gamma = 1</math> から <math>x_1 = 1/n</math>となる。 | ||
| − | + | 各個体の子孫がそれぞれ集団全体をカバーする可能性があり、各個体が均等な機会を持つから、これは当然の値ともいえる。 | |
| − | さて、確率 ''m'' | + | さて、確率 ''m'' でタイプBという突然変異が生じるとき、変異体Bの生じる個体数は ''mn'' になる。 |
各個体がそれぞれ集団をカバーしうるから、全てタイプAの集団からはじまって全てタイプBの集団に進化する速度は、<math>mn/n = m</math> となり、集団のサイズに依存しない。 | 各個体がそれぞれ集団をカバーしうるから、全てタイプAの集団からはじまって全てタイプBの集団に進化する速度は、<math>mn/n = m</math> となり、集団のサイズに依存しない。 | ||
ここから「分子時計」仮説が導かれる。 | ここから「分子時計」仮説が導かれる。 | ||
Revision as of 23:09, 23 June 2010
Contents |
出生死亡過程
モラン過程
個体数を n とし、状態 i から i+1, i-1 の状態へそれぞれ確率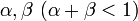 で遷移する場合を考える。
また状態 0 と n は吸収状態とする。(従ってユニークな定常分布を考えるわけではない。)
このマルコフ連鎖を1958年にモデルを発表した遺伝学者PAP MoranにちなんでMoran過程という。
で遷移する場合を考える。
また状態 0 と n は吸収状態とする。(従ってユニークな定常分布を考えるわけではない。)
このマルコフ連鎖を1958年にモデルを発表した遺伝学者PAP MoranにちなんでMoran過程という。
状態 i から出発して状態 n に到達する確率を 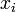 と書く。
と書く。
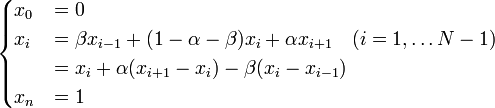
ここで記法
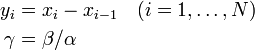
を導入すると

を得る。Moran過程では通常、少ない個体数からn個体にまで増殖するケースを考えるため、 は1より小さい値と考えてよい。
は1より小さい値と考えてよい。
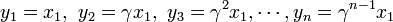
を足し合わせると
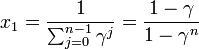
また
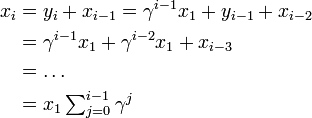
とあわせて
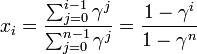
式の解釈
n 個体の集団において、全ての個体が最初タイプAであるとする。
このときタイプBという突然変異が1個生じたとする。
タイプBが 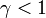 を満たす、すなわち
を満たす、すなわち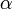 が
が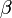 よりも大きくて個体数を増やす傾向にあると仮定する。
タイプBが何らかの優性種であると考えてもよい。
初めに1個生じたタイプBが集団 n の中に固定される(集団全体をカバーする)確率は
よりも大きくて個体数を増やす傾向にあると仮定する。
タイプBが何らかの優性種であると考えてもよい。
初めに1個生じたタイプBが集団 n の中に固定される(集団全体をカバーする)確率は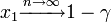 。
つまり、Aより10倍優位な変異体であっても (
。
つまり、Aより10倍優位な変異体であっても ( )、集団全体にその変異が保持される確率は 9/10 でしかない。
通常の遺伝子変異で生存戦略に極めて優性となるケースは非常に稀だとすれば、殆どの変異は集団全体に保持されないことになる。
)、集団全体にその変異が保持される確率は 9/10 でしかない。
通常の遺伝子変異で生存戦略に極めて優性となるケースは非常に稀だとすれば、殆どの変異は集団全体に保持されないことになる。
木村の中立進化説
突然変異が完全に中立な場合、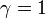 から
から  となる。
各個体の子孫がそれぞれ集団全体をカバーする可能性があり、各個体が均等な機会を持つから、これは当然の値ともいえる。
さて、確率 m でタイプBという突然変異が生じるとき、変異体Bの生じる個体数は mn になる。
各個体がそれぞれ集団をカバーしうるから、全てタイプAの集団からはじまって全てタイプBの集団に進化する速度は、
となる。
各個体の子孫がそれぞれ集団全体をカバーする可能性があり、各個体が均等な機会を持つから、これは当然の値ともいえる。
さて、確率 m でタイプBという突然変異が生じるとき、変異体Bの生じる個体数は mn になる。
各個体がそれぞれ集団をカバーしうるから、全てタイプAの集団からはじまって全てタイプBの集団に進化する速度は、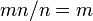 となり、集団のサイズに依存しない。
ここから「分子時計」仮説が導かれる。
となり、集団のサイズに依存しない。
ここから「分子時計」仮説が導かれる。