Aritalab:Lecture/NetworkBiology/Markov Chains/Birth-death Process
m |
m |
||
| Line 7: | Line 7: | ||
==出生死亡過程== | ==出生死亡過程== | ||
===モラン過程=== | ===モラン過程=== | ||
| − | 個体数を '' | + | 個体数を ''N'' とし、状態 ''i'' から ''i''+1, ''i''-1 の状態へそれぞれ確率<math>\alpha, \beta \ (\alpha + \beta < 1)</math>で遷移する場合を考える。 |
| − | また状態 0 と '' | + | また状態 0 と ''N'' は吸収状態とする。(従ってユニークな定常分布を考えるわけではない。) |
このマルコフ連鎖を1958年にモデルを発表した遺伝学者PAP MoranにちなんでMoran過程という。 | このマルコフ連鎖を1958年にモデルを発表した遺伝学者PAP MoranにちなんでMoran過程という。 | ||
| − | 状態 ''i'' から出発して状態 '' | + | 状態 ''i'' から出発して状態 ''N'' に到達する確率を <math>x_i</math> と書く。 |
<math> | <math> | ||
| Line 18: | Line 18: | ||
x_i &= \beta x_{i-1} + (1 - \alpha - \beta) x_i + \alpha x_{i+1} \quad (i = 1, \ldots N-1) \\ | x_i &= \beta x_{i-1} + (1 - \alpha - \beta) x_i + \alpha x_{i+1} \quad (i = 1, \ldots N-1) \\ | ||
&= x_i + \alpha (x_{i+1} - x_i) - \beta (x_i - x_{i-1}) \\ | &= x_i + \alpha (x_{i+1} - x_i) - \beta (x_i - x_{i-1}) \\ | ||
| − | + | x_N &= 1 \\ | |
\end{cases} | \end{cases} | ||
</math> | </math> | ||
| Line 33: | Line 33: | ||
を導入すると | を導入すると | ||
| − | <math>\textstyle y_{i+1} = \gamma y_i, \quad \sum^ | + | <math>\textstyle y_{i+1} = \gamma y_i, \quad \sum^N_{i=1} y_i = 1</math> |
| − | を得る。Moran過程では通常、少ない個体数から'' | + | を得る。Moran過程では通常、少ない個体数から''N''個体にまで増殖するケースを考えるため、<math>\gamma</math>は1より小さい値と考えてよい。 |
| − | <math> y_1 = x_1, \ y_2 = \gamma x_1, \ y_3 = \gamma^2 x_1, \cdots, y_n = \gamma^{ | + | <math> y_1 = x_1, \ y_2 = \gamma x_1, \ y_3 = \gamma^2 x_1, \cdots, y_n = \gamma^{N-1} x_1 </math> |
を足し合わせると | を足し合わせると | ||
<math> | <math> | ||
| − | x_1 = \frac{1}{\sum^{ | + | x_1 = \frac{1}{\sum^{N-1}_{j=0} \gamma^j} = \frac{1 - \gamma}{1 - \gamma^N} |
</math> | </math> | ||
| Line 59: | Line 59: | ||
<math> | <math> | ||
| − | x_i = \frac{\sum^{i-1}_{j=0} \gamma^j}{\sum^{ | + | x_i = \frac{\sum^{i-1}_{j=0} \gamma^j}{\sum^{N-1}_{j=0} \gamma^j} |
| − | = \frac{1 - \gamma^i}{1 - \gamma^ | + | = \frac{1 - \gamma^i}{1 - \gamma^N} |
</math> | </math> | ||
===式の解釈=== | ===式の解釈=== | ||
| − | '' | + | ''N'' 個体の集団において、全ての個体が最初タイプAであるとする。 |
このときタイプBという突然変異が1個生じたとする。 | このときタイプBという突然変異が1個生じたとする。 | ||
タイプBが <math>\gamma < 1</math>を満たす、すなわち<math>\alpha</math>が<math>\beta</math>よりも大きくて個体数を増やす傾向にあると仮定する。 | タイプBが <math>\gamma < 1</math>を満たす、すなわち<math>\alpha</math>が<math>\beta</math>よりも大きくて個体数を増やす傾向にあると仮定する。 | ||
タイプBが何らかの優性種であると考えてもよい。 | タイプBが何らかの優性種であると考えてもよい。 | ||
| − | 初めに1個生じたタイプBが集団 '' | + | 初めに1個生じたタイプBが集団 ''N'' の中に固定される(集団全体をカバーする)確率は<math>x_1 \xrightarrow{N \rightarrow \infty} 1 - \gamma</math>。 |
つまり、Aより10倍優位な変異体であっても (<math>\gamma = 1/10</math>)、集団全体にその変異が保持される確率は 9/10 でしかない。 | つまり、Aより10倍優位な変異体であっても (<math>\gamma = 1/10</math>)、集団全体にその変異が保持される確率は 9/10 でしかない。 | ||
通常の遺伝子変異で生存戦略に極めて優性となるケースは非常に稀だとすれば、殆どの変異は集団全体に保持されないことになる。 | 通常の遺伝子変異で生存戦略に極めて優性となるケースは非常に稀だとすれば、殆どの変異は集団全体に保持されないことになる。 | ||
| Line 76: | Line 76: | ||
ほとんどの遺伝子の突然変異は、自然淘汰において有利でも不利でもないとする[http://www.nig.ac.jp/museum_080501/evolution/C/bunsi-02.html 中立進化説]は当時大きな反響を呼んだ。 | ほとんどの遺伝子の突然変異は、自然淘汰において有利でも不利でもないとする[http://www.nig.ac.jp/museum_080501/evolution/C/bunsi-02.html 中立進化説]は当時大きな反響を呼んだ。 | ||
| − | 突然変異が完全に中立な場合、<math>\gamma = 1</math> から <math>x_1 = 1/ | + | 突然変異が完全に中立な場合、<math>\gamma = 1</math> から <math>x_1 = 1/N</math>となる。 |
各個体の子孫がそれぞれ集団全体をカバーする可能性があり、各個体が均等な機会を持つから、これは当然の値ともいえる。 | 各個体の子孫がそれぞれ集団全体をカバーする可能性があり、各個体が均等な機会を持つから、これは当然の値ともいえる。 | ||
| − | さて、確率 ''m'' でタイプBという突然変異が生じるとき、変異体Bの生じる個体数は '' | + | さて、確率 ''m'' でタイプBという突然変異が生じるとき、変異体Bの生じる個体数は ''mN'' になる。 |
| − | 各個体がそれぞれ集団をカバーしうるから、全てタイプAの集団からはじまって全てタイプBの集団に進化する速度は、<math> | + | 各個体がそれぞれ集団をカバーしうるから、全てタイプAの集団からはじまって全てタイプBの集団に進化する速度は、<math>mN/N = m</math> となり、集団のサイズに依存しない。 |
ここから「分子時計」仮説が導かれる。 | ここから「分子時計」仮説が導かれる。 | ||
==ネットワーク上の出生死亡過程== | ==ネットワーク上の出生死亡過程== | ||
モラン過程ではA個体とB個体の個数のみを考え、個体間のネットワークという概念が無かった。 | モラン過程ではA個体とB個体の個数のみを考え、個体間のネットワークという概念が無かった。 | ||
| − | ここでは '' | + | ここでは ''N'' 個体が遷移行列 <math>{\mathbf P}</math> であらわされるネットワークを考えよう。 |
各頂点は状態AまたはBをとり、単位時間にある頂点 ''i'' が隣接する頂点 ''j'' に確率 <math>p_{ij}</math> で自分の状態をコピーする。 | 各頂点は状態AまたはBをとり、単位時間にある頂点 ''i'' が隣接する頂点 ''j'' に確率 <math>p_{ij}</math> で自分の状態をコピーする。 | ||
また、BはAに比べ <math>1/r</math> の割合で選ばれる確率が高いとする。ここで扱うのは<math>0 \leq r \leq 1</math>の場合である。 | また、BはAに比べ <math>1/r</math> の割合で選ばれる確率が高いとする。ここで扱うのは<math>0 \leq r \leq 1</math>の場合である。 | ||
===モラン過程と同等なネットワーク=== | ===モラン過程と同等なネットワーク=== | ||
| − | 初めに1個体であったBが全体に広がる確率がMoran過程と同じ <math>(1-r)/(1-r^ | + | 初めに1個体であったBが全体に広がる確率がMoran過程と同じ <math>(1-r)/(1-r^N)</math> であるための条件を考えよう。 |
現在 ''m'' 頂点が状態B、残りが状態Aと仮定し、頂点 ''i'' が状態Bのとき <math>v_i = 1</math>, 状態Aのとき <math>v_i = 0</math>と書こう。 | 現在 ''m'' 頂点が状態B、残りが状態Aと仮定し、頂点 ''i'' が状態Bのとき <math>v_i = 1</math>, 状態Aのとき <math>v_i = 0</math>と書こう。 | ||
B個体が ''m''+1 に増える確率は、状態B (頂点 ''i'' とする)が選ばれて隣接する状態A (頂点 ''j'' とする) を上書きすればよいから | B個体が ''m''+1 に増える確率は、状態B (頂点 ''i'' とする)が選ばれて隣接する状態A (頂点 ''j'' とする) を上書きすればよいから | ||
| Line 108: | Line 108: | ||
個体 ''k'' ただ一つがBである特殊例 <math>v_k = 1,\ v_i = 0 (\forall i \neq k)</math> を考えると <math>\textstyle \sum_j p_{jk} = \sum_j p_{kj} = 1</math> となる。 | 個体 ''k'' ただ一つがBである特殊例 <math>v_k = 1,\ v_i = 0 (\forall i \neq k)</math> を考えると <math>\textstyle \sum_j p_{jk} = \sum_j p_{kj} = 1</math> となる。 | ||
| − | + | ただし右側の等号は、考えているネットワークがマルコフ連鎖であるため、頂点から出る辺確率の和が1であることから導かれる。 | |
| − | + | つまり、定常分布での存在確率が全頂点において等しいときには(別の言葉でいうと、全頂点が対等な関係にある場合は)、Moran過程と同じプロセスになる。 | |
| − | + | 定常分布での存在確率が全頂点で等しくなるのは、接続関係が対称なネットワークだけに限らず、非対称な場合もありうることに注意しよう。 | |
例えば一方向にのみ遷移する環状ネットワークは方向性を持つので非対称だがMoran過程と同等になる。 | 例えば一方向にのみ遷移する環状ネットワークは方向性を持つので非対称だがMoran過程と同等になる。 | ||
| Line 124: | Line 124: | ||
結果から先に言うと、固定確率は <math>\textstyle x_i = \frac{1-r^{2i}}{1-r^{2n}}</math> であらわされる。 | 結果から先に言うと、固定確率は <math>\textstyle x_i = \frac{1-r^{2i}}{1-r^{2n}}</math> であらわされる。 | ||
| − | + | 星型の枝が非常に多い場合を考え、周囲の頂点には状態Bが ''m'' 個、状態Aが ''N-m'' 個あると仮定しよう。 | |
周囲の頂点で状態Bを増やすには、中央の頂点が状態Bの際に選択されねばならず、 | 周囲の頂点で状態Bを増やすには、中央の頂点が状態Bの際に選択されねばならず、 | ||
周囲の頂点で状態Aを増やすには、中央の頂点が状態Aの際に選択されねばならない。 | 周囲の頂点で状態Aを増やすには、中央の頂点が状態Aの際に選択されねばならない。 | ||
| − | 中央の頂点は状態BとAの間を行き来するが、状態Bのほうが<math>1/r</math>倍選択されやすい。 | + | 中央の頂点は状態BとAの間を行き来するが、状態Bのほうが <math>1/r</math> 倍選択されやすい。 |
| − | 中央の頂点が状態Bにいるほうが<math>1/r</math>倍選択されやすく、更に中央の頂点の状態にかかわらず周囲の頂点のうちBが選択されるほうが<math>1/r</math>倍多いため、結果としてBが<math>1/r^2</math>倍選択されることになる。 | + | 中央の頂点が状態Bにいるほうが <math>1/r</math> 倍選択されやすく、更に中央の頂点の状態にかかわらず周囲の頂点のうちBが選択されるほうが <math>1/r</math> 倍多いため、結果としてBが <math>1/r^2</math> 倍選択されることになる。 |
つまり | つまり | ||
<math>\textstyle \frac{B_{m\rightarrow (m-1)}}{B_{m\rightarrow (m+1)}} | <math>\textstyle \frac{B_{m\rightarrow (m-1)}}{B_{m\rightarrow (m+1)}} | ||
| − | + | = r^2 </math> | |
| − | + | 適応度がMoran過程に比べて <math>r^2</math> に増幅されていることがわかる。 | |
==ネットワーク上のゲーム== | ==ネットワーク上のゲーム== | ||
Revision as of 16:46, 24 June 2010
Contents |
参考文献
- Lieberman E,Hauert C, Nowak MA (2005) Evolutionary Dynamics on Graphs. Nature 433:312-316
- Nowak MA (2006) Evolutionary Dynamics: Exploring the Equations of Life, Belknap Press of Harvard University Press
出生死亡過程
モラン過程
個体数を N とし、状態 i から i+1, i-1 の状態へそれぞれ確率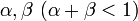 で遷移する場合を考える。
また状態 0 と N は吸収状態とする。(従ってユニークな定常分布を考えるわけではない。)
このマルコフ連鎖を1958年にモデルを発表した遺伝学者PAP MoranにちなんでMoran過程という。
で遷移する場合を考える。
また状態 0 と N は吸収状態とする。(従ってユニークな定常分布を考えるわけではない。)
このマルコフ連鎖を1958年にモデルを発表した遺伝学者PAP MoranにちなんでMoran過程という。
状態 i から出発して状態 N に到達する確率を 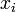 と書く。
と書く。
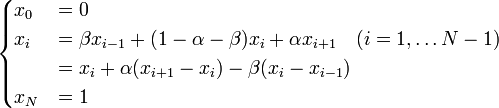
ここで記法
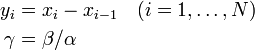
を導入すると

を得る。Moran過程では通常、少ない個体数からN個体にまで増殖するケースを考えるため、 は1より小さい値と考えてよい。
は1より小さい値と考えてよい。
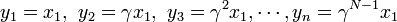
を足し合わせると
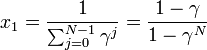
また
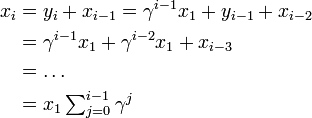
とあわせて

式の解釈
N 個体の集団において、全ての個体が最初タイプAであるとする。
このときタイプBという突然変異が1個生じたとする。
タイプBが 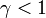 を満たす、すなわち
を満たす、すなわち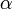 が
が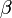 よりも大きくて個体数を増やす傾向にあると仮定する。
タイプBが何らかの優性種であると考えてもよい。
初めに1個生じたタイプBが集団 N の中に固定される(集団全体をカバーする)確率は
よりも大きくて個体数を増やす傾向にあると仮定する。
タイプBが何らかの優性種であると考えてもよい。
初めに1個生じたタイプBが集団 N の中に固定される(集団全体をカバーする)確率は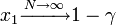 。
つまり、Aより10倍優位な変異体であっても (
。
つまり、Aより10倍優位な変異体であっても ( )、集団全体にその変異が保持される確率は 9/10 でしかない。
通常の遺伝子変異で生存戦略に極めて優性となるケースは非常に稀だとすれば、殆どの変異は集団全体に保持されないことになる。
)、集団全体にその変異が保持される確率は 9/10 でしかない。
通常の遺伝子変異で生存戦略に極めて優性となるケースは非常に稀だとすれば、殆どの変異は集団全体に保持されないことになる。
木村資生の中立進化説
木村資生(きむらもとお)は1970年代に活躍した国立遺伝学研究所の研究者である。 ほとんどの遺伝子の突然変異は、自然淘汰において有利でも不利でもないとする中立進化説は当時大きな反響を呼んだ。
突然変異が完全に中立な場合、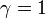 から
から 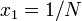 となる。
各個体の子孫がそれぞれ集団全体をカバーする可能性があり、各個体が均等な機会を持つから、これは当然の値ともいえる。
さて、確率 m でタイプBという突然変異が生じるとき、変異体Bの生じる個体数は mN になる。
各個体がそれぞれ集団をカバーしうるから、全てタイプAの集団からはじまって全てタイプBの集団に進化する速度は、
となる。
各個体の子孫がそれぞれ集団全体をカバーする可能性があり、各個体が均等な機会を持つから、これは当然の値ともいえる。
さて、確率 m でタイプBという突然変異が生じるとき、変異体Bの生じる個体数は mN になる。
各個体がそれぞれ集団をカバーしうるから、全てタイプAの集団からはじまって全てタイプBの集団に進化する速度は、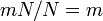 となり、集団のサイズに依存しない。
ここから「分子時計」仮説が導かれる。
となり、集団のサイズに依存しない。
ここから「分子時計」仮説が導かれる。
ネットワーク上の出生死亡過程
モラン過程ではA個体とB個体の個数のみを考え、個体間のネットワークという概念が無かった。
ここでは N 個体が遷移行列 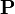 であらわされるネットワークを考えよう。
各頂点は状態AまたはBをとり、単位時間にある頂点 i が隣接する頂点 j に確率
であらわされるネットワークを考えよう。
各頂点は状態AまたはBをとり、単位時間にある頂点 i が隣接する頂点 j に確率 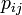 で自分の状態をコピーする。
また、BはAに比べ
で自分の状態をコピーする。
また、BはAに比べ 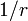 の割合で選ばれる確率が高いとする。ここで扱うのは
の割合で選ばれる確率が高いとする。ここで扱うのは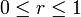 の場合である。
の場合である。
モラン過程と同等なネットワーク
初めに1個体であったBが全体に広がる確率がMoran過程と同じ 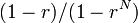 であるための条件を考えよう。
現在 m 頂点が状態B、残りが状態Aと仮定し、頂点 i が状態Bのとき
であるための条件を考えよう。
現在 m 頂点が状態B、残りが状態Aと仮定し、頂点 i が状態Bのとき 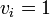 , 状態Aのとき
, 状態Aのとき 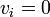 と書こう。
B個体が m+1 に増える確率は、状態B (頂点 i とする)が選ばれて隣接する状態A (頂点 j とする) を上書きすればよいから
と書こう。
B個体が m+1 に増える確率は、状態B (頂点 i とする)が選ばれて隣接する状態A (頂点 j とする) を上書きすればよいから
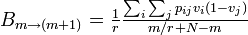
同様に、m-1 に減少する確率は
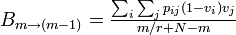
Moran過程と同等になるには各頂点の状態に非依存で

が成立せねばならず
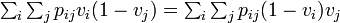
個体 k ただ一つがBである特殊例  を考えると
を考えると 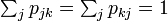 となる。
ただし右側の等号は、考えているネットワークがマルコフ連鎖であるため、頂点から出る辺確率の和が1であることから導かれる。
つまり、定常分布での存在確率が全頂点において等しいときには(別の言葉でいうと、全頂点が対等な関係にある場合は)、Moran過程と同じプロセスになる。
となる。
ただし右側の等号は、考えているネットワークがマルコフ連鎖であるため、頂点から出る辺確率の和が1であることから導かれる。
つまり、定常分布での存在確率が全頂点において等しいときには(別の言葉でいうと、全頂点が対等な関係にある場合は)、Moran過程と同じプロセスになる。
定常分布での存在確率が全頂点で等しくなるのは、接続関係が対称なネットワークだけに限らず、非対称な場合もありうることに注意しよう。 例えば一方向にのみ遷移する環状ネットワークは方向性を持つので非対称だがMoran過程と同等になる。
固定確率を低めるネットワーク
いかに優性な個体Bが生じても、固定確率が中立進化の場合に同じ 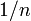 となるネットワークは簡単に構成できる。
例えば既約なネットワークに根 (root) となる頂点を一つ付け足した場合を考えれば、根にあたる頂点に優性な変異Bが生じないと固定されないので固定確率が
となるネットワークは簡単に構成できる。
例えば既約なネットワークに根 (root) となる頂点を一つ付け足した場合を考えれば、根にあたる頂点に優性な変異Bが生じないと固定されないので固定確率が 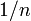 となる。同じ理由で、根にあたる頂点が複数あるネットワークは決して固定されることがない。
となる。同じ理由で、根にあたる頂点が複数あるネットワークは決して固定されることがない。
固定確率を高めるネットワーク
ここでは星型 (star) のネットワークはMoran過程より固定確率が高くなることを説明する。
結果から先に言うと、固定確率は 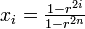 であらわされる。
であらわされる。
星型の枝が非常に多い場合を考え、周囲の頂点には状態Bが m 個、状態Aが N-m 個あると仮定しよう。
周囲の頂点で状態Bを増やすには、中央の頂点が状態Bの際に選択されねばならず、
周囲の頂点で状態Aを増やすには、中央の頂点が状態Aの際に選択されねばならない。
中央の頂点は状態BとAの間を行き来するが、状態Bのほうが 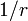 倍選択されやすい。
中央の頂点が状態Bにいるほうが
倍選択されやすい。
中央の頂点が状態Bにいるほうが 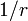 倍選択されやすく、更に中央の頂点の状態にかかわらず周囲の頂点のうちBが選択されるほうが
倍選択されやすく、更に中央の頂点の状態にかかわらず周囲の頂点のうちBが選択されるほうが 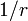 倍多いため、結果としてBが
倍多いため、結果としてBが 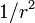 倍選択されることになる。
倍選択されることになる。
つまり

適応度がMoran過程に比べて 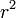 に増幅されていることがわかる。
に増幅されていることがわかる。
ネットワーク上のゲーム
各頂点は 協力 (C: Cooperate) か裏切り (D: Defect) のいずれかの戦略を取るとする。 協力者は隣接頂点それぞれにコスト (cost) c を支払い、隣接する頂点は利得 (benefit) b を受け取る。 裏切る場合はコストを払わず、隣からの利得のみを受け取る。 頂点の適応度 (fitness) を支払いと利得の合計で判断し、戦略を更新する方法として以下の2通りを考えよう。
- 出生死亡過程: 単位時間毎に適応度に応じて頂点を選択し、隣接頂点をランダムに選んで同じ戦略へとコピーする。
- 死亡出生過程: 単位時間毎に頂点がランダムに選ばれて死亡する。隣接する頂点がそれぞれの適応度に応じて自分の戦略をその頂点にコピーする。
もっとも単純なケースとして単純サイクルを考える。
- 出生死亡過程の場合
- C戦略とD戦略をとる頂点の境界部分にある2頂点を考慮すればよい。
C戦略の端にいる頂点は、隣接する2頂点分のコストを払って利得を片側からしか得ないので合計は 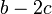 になるが、D戦略の端にいる頂点は利得 b を得られるので、いかなる b, c であってもD戦略が優位になる。
になるが、D戦略の端にいる頂点は利得 b を得られるので、いかなる b, c であってもD戦略が優位になる。
- 死亡出生過程の場合
- C戦略とD戦略をとる頂点の境界部分から2つ離れたところまでの合計4頂点を考慮する。
D戦略を取る側は、C戦略と隣接する頂点が b、そのまた隣は 0 になる。
C戦略を取る側は、D戦略と隣接する頂点が 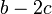 、そのまた隣は
、そのまた隣は 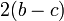 になる。
従って
になる。
従って 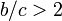 の場合はC戦略が優位。
一般化すると、次数 k の格子であれば
の場合はC戦略が優位。
一般化すると、次数 k の格子であれば 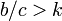 の場合にC戦略が優位になる。
の場合にC戦略が優位になる。