Aritalab:Lecture/Biochem/Protein
m (→ラマチャンドランプロット) |
m (→構造の分類と測定) |
||
| (5 intermediate revisions by one user not shown) | |||
| Line 5: | Line 5: | ||
==タンパク質のみかた== | ==タンパク質のみかた== | ||
| − | + | タンパク質は20種類の[[Aritalab:Lecture/Biochem/Amino_Acid|アミノ酸]]が連なったポリペプチドです。 | |
タンパク質を大きく分けると表のようになります。 | タンパク質を大きく分けると表のようになります。 | ||
| Line 90: | Line 90: | ||
ラマチャンドラン (Gopalasamudram Narayana Ramachandran) は、インド出身の生物物理学者です。 | ラマチャンドラン (Gopalasamudram Narayana Ramachandran) は、インド出身の生物物理学者です。 | ||
| − | ペプチド鎖の特徴をみるのに、各アミノ酸のφ角度とψ角度を平面にプロットする方法を考え出しました。角度はそれぞれα炭素からアミノ基(C-N結合)とカルボキシル基(C-C結合)を見たとき時計回りに何度ねじれているかを表現しています。180°ずれると互い違いのトランス配置を取ると憶えておくと楽です。タンパク質構造の場合、ペプチド結合の平面が互い違いに平面に揃う場合が& | + | ペプチド鎖の特徴をみるのに、各アミノ酸のφ角度とψ角度を平面にプロットする方法を考え出しました。角度はそれぞれα炭素からアミノ基(C-N結合)とカルボキシル基(C-C結合)を見たとき時計回りに何度ねじれているかを表現しています。180°ずれると互い違いのトランス配置を取ると憶えておくと楽です。タンパク質構造の場合、ペプチド結合の平面が互い違いに平面に揃う場合が±180°です。 |
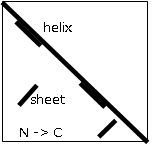
二面角をプロットするとへリックスとシート構造がきれいに分離され、タンパク質の構造分類に使えます。 | 二面角をプロットするとへリックスとシート構造がきれいに分離され、タンパク質の構造分類に使えます。 | ||
| Line 101: | Line 101: | ||
==コンタクトマップ== | ==コンタクトマップ== | ||
| + | [[File:JSBi-contactmap.png|right]] | ||
縦(上から下にN→C)横(左から右にN→C)にペプチド鎖を並べ、C<sub>α</sub>原子間の距離が10オングストローム以内であれば色を塗ったものをコンタクトマップと呼びます。 | 縦(上から下にN→C)横(左から右にN→C)にペプチド鎖を並べ、C<sub>α</sub>原子間の距離が10オングストローム以内であれば色を塗ったものをコンタクトマップと呼びます。 | ||
| − | 対角線は同一の残基がくるので黒くなります。α- | + | 対角線は同一の残基がくるので黒くなります。α-へリックスは、およそ3.6残基で一周してその径が12オングストローム程度なので、この対角線上に重なるように表示されます。 |
| − | + | ||
| + | 平行β-シートは対角線から離れた位置に対角線と同じ角度で現れます。逆平行β-シートの場合、向きが逆になるので対角線と直行する角度に現れます。 | ||
==構造の分類と測定== | ==構造の分類と測定== | ||
| − | タンパク質立体構造の研究はミオグロビン(myoglobin: 筋肉にある赤いタンパク質)から始まりました。ジョン・ケンドリュー(John Kendrew) | + | タンパク質立体構造の研究はミオグロビン(myoglobin: 筋肉にある赤いタンパク質)から始まりました。ジョン・ケンドリュー(John Kendrew)がX線回折で世界ではじめてタンパク質の構造を明らかにしたのは1960年です(そんなに昔ではないのです。予測した構造の |
| + | 写真が[http://www2.mrc-lmb.cam.ac.uk/photo-archive/john-kendrew-lecturing/ ここ]にあります。)。立体構造解析に対する功績により、ケンドリューはわずか2年後の1962年にノーベル化学賞を授与されています(ペルーツと共同)。 | ||
[[Image:Lecture-biochem-protein-myoglobin.jpg|thumb|PDB (1mbn) Myoglobin]] | [[Image:Lecture-biochem-protein-myoglobin.jpg|thumb|PDB (1mbn) Myoglobin]] | ||
| Line 113: | Line 115: | ||
DNAに比較すると、タンパク質の構造は遥かに複雑で理解が難しいものでした。 | DNAに比較すると、タンパク質の構造は遥かに複雑で理解が難しいものでした。 | ||
| − | 現在、タンパク質の構造は、長さが 50- | + | 現在、タンパク質の構造は、長さが 50-150アミノ酸程度(平均100)のドメインと呼ばれるブロックに分けて考えます。各ドメインは機能部位や疎水性コアを持ち、ドメイン間の二次構造どうしは近接しません。ドメインとはつまり、タンパク質の構造(および機能)モジュールと捉えられます。金属イオンと結合して構造を形成するドメイン(例. ジンクフィンガー)もあります。 |
Latest revision as of 19:55, 15 November 2019
|
[edit] タンパク質のみかた
タンパク質は20種類のアミノ酸が連なったポリペプチドです。
タンパク質を大きく分けると表のようになります。
| 水溶性タンパク | 球状 (globular) | 酵素や転写因子で、細胞質のようなゾル内で機能するタンパク質です。分子内部は疎水性、外部は親水性アミノ酸が分布しています。 |
| 不定形 (disordered) | 真核生物に多い構造不定のタンパク質です。親水性アミノ酸(とりわけKEPQRS)が多く、転写因子などの相互作用にその性質が利用されるといわれています。 | |
| 膜タンパク | 受容体、トランスポーターなど、脂質二重膜に付着したり埋没した形で機能するタンパク質です。疎水性アミノ酸が多く、とりわけ膜貫通領域は疎水性です。全タンパク質の 3 割ほどを占めるにもかかわらず、結晶化しにくく構造がほとんどわかっていません。 | |
[edit] アミノ酸指標
Kyte と Doolittle は 1982 年に疎水性スケール (hydropathy scale) というアミノ酸毎の疎水度を求めました。[1] アミノ酸配列をこの数値に変換し、5 から 7 残基のウィンドウで平均化するとタンパク質表面にある領域を予測できます。またウィンドウを 19 から 21 残基にとることで膜貫通領域の予測もできます。(後者の場合、平均値が 1.6 以上が目安とされています。)
この後、様々な類似の指標が発表されました。例えばHopp-Woods指標は抗体の抗原部分を予測するために発表されたもので基本的に Kyte-Doolittle の符号が逆転している事がわかります。[2]また Engelman 指標は Kyte-Doolittle と同様に疎水性の指標として現在も使われています。[3] Kyte-Doolittle とは、S, T, W などの値が異なるところが特徴です。これらで計算される値はあくまで「傾向」であり、正確に予測するものではありません。
何百と発表されてきたアミノ酸指標は、AAIndex データベースで検索可能です。
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[edit] ラマチャンドランプロット
|
アミノ酸配列は、ペプチド結合における二面角のリスト φ1, ψ1, φ2, ψ2, ..., φN, ψN で表すことができます。 この値を平面に散布図としてプロットしたものをラマチャンドラン (Ramachandran) プロットと呼びます。 ラマチャンドラン (Gopalasamudram Narayana Ramachandran) は、インド出身の生物物理学者です。 ペプチド鎖の特徴をみるのに、各アミノ酸のφ角度とψ角度を平面にプロットする方法を考え出しました。角度はそれぞれα炭素からアミノ基(C-N結合)とカルボキシル基(C-C結合)を見たとき時計回りに何度ねじれているかを表現しています。180°ずれると互い違いのトランス配置を取ると憶えておくと楽です。タンパク質構造の場合、ペプチド結合の平面が互い違いに平面に揃う場合が±180°です。 二面角をプロットするとへリックスとシート構造がきれいに分離され、タンパク質の構造分類に使えます。
|
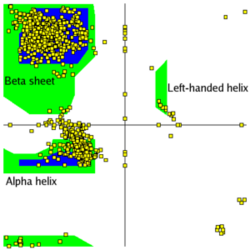 (図はウィキペディアより) (図はウィキペディアより)
|
[edit] コンタクトマップ
縦(上から下にN→C)横(左から右にN→C)にペプチド鎖を並べ、Cα原子間の距離が10オングストローム以内であれば色を塗ったものをコンタクトマップと呼びます。 対角線は同一の残基がくるので黒くなります。α-へリックスは、およそ3.6残基で一周してその径が12オングストローム程度なので、この対角線上に重なるように表示されます。
平行β-シートは対角線から離れた位置に対角線と同じ角度で現れます。逆平行β-シートの場合、向きが逆になるので対角線と直行する角度に現れます。
[edit] 構造の分類と測定
タンパク質立体構造の研究はミオグロビン(myoglobin: 筋肉にある赤いタンパク質)から始まりました。ジョン・ケンドリュー(John Kendrew)がX線回折で世界ではじめてタンパク質の構造を明らかにしたのは1960年です(そんなに昔ではないのです。予測した構造の 写真がここにあります。)。立体構造解析に対する功績により、ケンドリューはわずか2年後の1962年にノーベル化学賞を授与されています(ペルーツと共同)。
DNAに比較すると、タンパク質の構造は遥かに複雑で理解が難しいものでした。
現在、タンパク質の構造は、長さが 50-150アミノ酸程度(平均100)のドメインと呼ばれるブロックに分けて考えます。各ドメインは機能部位や疎水性コアを持ち、ドメイン間の二次構造どうしは近接しません。ドメインとはつまり、タンパク質の構造(および機能)モジュールと捉えられます。金属イオンと結合して構造を形成するドメイン(例. ジンクフィンガー)もあります。
立体構造を分類するデータベースには、手作業で構造を分けた SCOP (structural classification of proteins) や CATH があります。いずれもドメインを考慮した分類を採用しており、大きく分けると以下のようになります。(図はCATH DBより)より詳しくは 構造のページをみてください。
mainly α
|
mainly β
|
α and β
|
few structures
|
[edit] 測定方法
- ゲル電気泳動
タンパク質は帯電しているので、ポリアクリルアミド電気泳動 (PAGE) で分離できます。
- X線回折
タンパク質を結晶化させられる場合はX線結晶解析により原子位置を特定できます。 粒子加速器から得られるX線を用いると、Cαほか、重い原子の位置を計算できます。水素の位置はわかりません。
- NMR解析
NMRとはNuclear Magnetic Resonanceの略で、原子核の磁気共鳴を用いて原子の位置を特定します。
- 参考
- ↑ Kyte J, Doolittle R (1982) "A simple method for displaying the hydropathic character of a protein" J Mol Biol 157:105-132
- ↑ Hopp TP, Woods KR (1983) "A computer program for predicting protein antigenic determinants" Mol Immunol 20(4):483-489
- ↑ Engelman DM, Steitz TA, Goldman A (1986) "Identifying nonpolar transbilayer helices in amino acid sequences of membrane proteins" Annu Rev Biophys Biophys Chem 15:321-353