Aritalab:Lecture/Basic/Expectation

From Metabolomics.JP
< Aritalab:Lecture | Basic(Difference between revisions)
Jump to: navigation, search
m
m
Line 1: Line 1:
 
==期待値・平均==
 
==期待値・平均==
  
−
===定義 E[確率変数] = Xの値とその値をとる確率の総和 ===
+
;定義: E[確率変数] = Xの値とその値をとる確率の総和
−
期待値とは、確率変数（例えばサイコロ）の取る値とその確率とをかけた総和です。
+
−
通常「平均」というと、全ての要素が等確率で生じているという前提があるので、数学では期待値という言葉を使います。期待値は英語でExpectationなので E[確率変数] と書きます。
+
  
−
;例 フェアなサイコロの期待値
+
期待値とは、確率変数（例えばサイコロ）の取る値とその確率とをかけた総和です。 通常「平均」というと、全ての要素が等確率で生じているという前提があるので、数学では期待値という言葉を使います。期待値は英語でExpectationなので E[確率変数] と書きます。
 +
 
 +
:例. フェアなサイコロの期待値
 
: E[サイコロ] = 1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 3.5
 
: E[サイコロ] = 1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 3.5
 
: E[フェアなコインで表が出る] = 1 * 1/2 + 0 * 1/2 = 0.5
 
: E[フェアなコインで表が出る] = 1 * 1/2 + 0 * 1/2 = 0.5
 +
 
コインのときは、表が出たら1, 裏が出たら0として計算しています。
 
コインのときは、表が出たら1, 裏が出たら0として計算しています。
  
−
=== E[nX] = n E[X] (n: 実数) ===
+
; E[''n'' X] = ''n'' E[X] (''n'' ... 実数)
 
期待値は確率変数の値の和をとっているだけなので、変数の値が全てn倍されたら期待値もn倍されます。
 
期待値は確率変数の値の和をとっているだけなので、変数の値が全てn倍されたら期待値もn倍されます。
  
−
=== E[X+Y]=E[X]+E[Y] ===
+
; E[X+Y] = E[X] + E[Y]
  
−
二つの確率変数X,Yがあったとき、和の期待値は、期待値の和に等しいという性質は、確率変数が互いに独立でなくても成立します。期待値の定義を良く考えると確率の足し算をしているだけですから、和について「くくりだし」が可能です。
+
二つの確率変数 ''X, Y'' があったとき、和の期待値は、期待値の和に等しいという性質は、確率変数が互いに独立でなくても成立します。期待値の定義を考えると確率の足し算をしているだけですから、和について「くくりだし」が可能です。
  
−
確率変数という言葉がわかりにくい場合は、サイコロと考えてください。二つのサイコロの目を足した数の期待値（平均）は、個々のサイコロの期待値（平均）の和ということです。例えば、サイコロ2個を振って出る目を足した数の平均値を数え上げて求めるのは、目の組み合わせが1,1の場合から6,6の場合まで数え上げなくてはならず大変です。
+
確率変数という言葉がわかりにくい場合は、サイコロを考えてください。二つのサイコロの目を足した数の期待値（平均）は、個々のサイコロの期待値（平均）の和ということです。例えば、サイコロ2個を振って出る目を足した数の平均値を数え上げて求めるのは、目の組み合わせが1,1の場合から6,6の場合まで数え上げなくてはならず大変です。
 
しかし、上の式を用いれば簡単に求められます。
 
しかし、上の式を用いれば簡単に求められます。
  
−
;例 サイコロ2個の和の期待値
+
:例. サイコロ2個の和の期待値
 
: E[サイコロ2個の和] = E[サイコロ1個] + E[サイコロ1個] = 3.5 + 3.5 = 7
 
: E[サイコロ2個の和] = E[サイコロ1個] + E[サイコロ1個] = 3.5 + 3.5 = 7
 
: E[コイン10枚で表が出る] = 10 * E[コイン1枚] = 10 * 1/2 = 5
 
: E[コイン10枚で表が出る] = 10 * E[コイン1枚] = 10 * 1/2 = 5
Line 27: Line 28:
 
二つのサイコロが''独立''のときに限り、期待値は積についても分配できます。
 
二つのサイコロが''独立''のときに限り、期待値は積についても分配できます。
  
−
;例 サイコロ2個の積の期待値
+
:例. サイコロ2個の積の期待値
 
:E[サイコロ2個の積] = ( E[サイコロ1個] )<sup>2</sup> = (3.5)<sup>2</sup> = 12.25
 
:E[サイコロ2個の積] = ( E[サイコロ1個] )<sup>2</sup> = (3.5)<sup>2</sup> = 12.25
 
:E[コイン2枚の積] = ( E[コイン1枚] )<sup>2</sup> = (1/2)<sup>2</sup> = 0.25
 
:E[コイン2枚の積] = ( E[コイン1枚] )<sup>2</sup> = (1/2)<sup>2</sup> = 0.25
Line 33: Line 34:
  
 
==分散==
 
==分散==
−
確率変数（例えばサイコロ）がとる値のばらつきの度合いを分散といいます。
+
確率変数（例えばサイコロ）がとる値のばらつきの度合いを分散といいます。　分散は英語でVarianceなので V[確率変数] と書きます。
−
分散は英語でVarianceなので V[確率変数] と書きます。
+
  
−
===定義: V[X] = E[(X-E[X])<sup>2</sup>] = E[X<sup>2</sup>] -(E[X])<sup>2</sup>===
+
; 定義: V[X] = E[(X-E[X])<sup>2</sup>] = E[X<sup>2</sup>] -(E[X])<sup>2</sup>
  
 
二つ目の等式は以下のようにして成立します。
 
二つ目の等式は以下のようにして成立します。
Line 50: Line 50:
 
</math>
 
</math>
  
−
;例　フェアなサイコロの分散
+
:例.　フェアなサイコロの分散
 
: V[サイコロ] = <math>((1-3.5)^2+(2-3.5)^2+(3-3.5)^2+(4-3.5)^2+(5-3.5)^2+(6-3.5)^2)/6</math> = 35/12 (≒ 2.916)
 
: V[サイコロ] = <math>((1-3.5)^2+(2-3.5)^2+(3-3.5)^2+(4-3.5)^2+(5-3.5)^2+(6-3.5)^2)/6</math> = 35/12 (≒ 2.916)
  
−
=== V[nX] = n<sup>2</sup>V[X] (n: 実数)===
+
; V[''n'' X] = ''n''<sup>2</sup> V[X] (''n'' ... 実数)
  
−
;証明
+
:証明
 
: <math>
 
: <math>
 
\begin{alignat}{2}
 
\begin{alignat}{2}
Line 64: Line 64:
 
</math>
 
</math>
  
−
;例　サイコロの目の2倍の分散
+
:例.　サイコロの目の2倍の分散
 
:サイコロの目の2倍は、2個のサイコロの目を足したものとは違うことに注意しましょう。目を2倍しても、例えば奇数の値は決して出てきません。
 
:サイコロの目の2倍は、2個のサイコロの目を足したものとは違うことに注意しましょう。目を2倍しても、例えば奇数の値は決して出てきません。
 
:V[2*サイコロ] = 4 * 35 / 12 = 35 / 3
 
:V[2*サイコロ] = 4 * 35 / 12 = 35 / 3
  
−
=== V[X+Y] = V[X] + V[Y] (ただしX,Yは独立) ===
+
;V[X+Y] = V[X] + V[Y] (ただし X,Y は独立)
  
−
X,Yが独立であれば、和の分散は分散の和に等しくなります。しかし独立でない場合には V[X+Y] > V[X] + V[Y] です。この「ズレ」を共分散と呼びます。
+
X,Y が独立であれば、和の分散は分散の和に等しくなります。しかし独立でない場合には V[X+Y] > V[X] + V[Y] です。この「ズレ」部分を共分散 (covariance) と呼びます。
−
:<math>V[X+Y] = V[X] + V[Y] + 2Cov[X,Y]</math>
+
  
−
;例　2個のサイコロの目の和の分散
+
: V[X+Y] = V[X] + V[Y] + 2Cov[X,Y]
 +
 
 +
:例　2個のサイコロの目の和の分散
 
:V[サイコロ+サイコロ] = 35/12 + 35/12 = 35/6
 
:V[サイコロ+サイコロ] = 35/12 + 35/12 = 35/6
  
−
サイコロを1個振ってその目を二倍した場合、2から12までの偶数が等確率(1/6)で出てきます。しかし2個のサイコロの和の場合、同じく2から12までの数が出てきますが、2や12はそれぞれ1/36の確率です。6は(1,5) (2,4) (3,3) (4,2) (5,1)という組み合わせがありうるので5/36の確率で出てきます。つまり、6や7という平均的な値が出やすくなっているので、目の二倍よりも分散は小さくなります。
+
サイコロを1個振ってその目を二倍した場合、2から12までの偶数が等確率(1/6)で出てきます。しかし2個のサイコロの和の場合、同じく2から12までの数が出てきますが、2や12はそれぞれ1/36の確率です。6は(1,5) (2,4) (3,3) (4,2) (5,1)という組み合わせがありうるので5/36の確率で出てきます。つまり、6や7という平均的な値が出やすくなっているので、目の二倍よりも分散が小さくなります。
  
−
===複数のサイコロの目の平均の分散===
+
:例 複数のサイコロの目の平均の分散
  
−
ここで応用例として、n個のサイコロを振ったときの、目の平均値の分散を考えてみましょう。個々のサイコロの目の期待値は7/2です。n個の平均の期待値は7/2のまま変わりません。しかし分散は違います。n個のサイコロの目の和の分散を計算してみましょう。ここではサイコロをXと記述します。
+
ここで応用例として、''n'' 個のサイコロを振ったときの、目の平均値の分散を考えてみましょう。個々のサイコロの目の期待値は7/2です。''n'' 個の平均の期待値は7/2のまま変わりません。しかし分散は違います。''n'' 個のサイコロの目の和の分散を計算してみましょう。ここではサイコロを X と記述します。
  
 
:V[(X<sub>1</sub>+X<sub>2</sub>+ ... X<sub>n</sub>)/n]  
 
:V[(X<sub>1</sub>+X<sub>2</sub>+ ... X<sub>n</sub>)/n]  
Line 90: Line 91:
  
 
==共分散==
 
==共分散==
−
共分散は二組の対応する確率変数の間で、ばらつきが異なる度合いです。数式にすると、Xにおいて平均からズレた量とYにおいて平均からズレた量を掛け算して平均したものにあたります。
+
共分散 (covariance) は二組の対応する確率変数の間で、ばらつきが異なる度合いです。数式にすると、Xにおいて平均からズレた量とYにおいて平均からズレた量を掛け算して平均したものにあたります。
  
−
=== 定義: Cov[X,Y]=E[(X-E[X])(Y-E[Y])] = E[XY] - E[X]E[Y] ===
+
;定義: Cov[X,Y]=E[(X-E[X])(Y-E[Y])] = E[XY] - E[X]E[Y]
  
 
等式の二つ目は、分散の定義における証明と同じ理由で成立します。
 
等式の二つ目は、分散の定義における証明と同じ理由で成立します。
Line 105: Line 106:
 
==相関==
 
==相関==
 
共分散をXの標準偏差とYの標準偏差で割ったものが相関係数です。
 
共分散をXの標準偏差とYの標準偏差で割ったものが相関係数です。
 +
 
:<math>Corr[X,Y] = Cov[X,Y] /(V[X]^{1/2}V[Y]^{1/2})</math>
 
:<math>Corr[X,Y] = Cov[X,Y] /(V[X]^{1/2}V[Y]^{1/2})</math>

Revision as of 14:34, 19 May 2011

Contents

期待値・平均

定義
E[確率変数] = Xの値とその値をとる確率の総和

期待値とは、確率変数（例えばサイコロ）の取る値とその確率とをかけた総和です。 通常「平均」というと、全ての要素が等確率で生じているという前提があるので、数学では期待値という言葉を使います。期待値は英語でExpectationなので E[確率変数] と書きます。

例. フェアなサイコロの期待値
E[サイコロ] = 1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 3.5
E[フェアなコインで表が出る] = 1 * 1/2 + 0 * 1/2 = 0.5

コインのときは、表が出たら1, 裏が出たら0として計算しています。

E[n X] = n E[X] (n ... 実数)

期待値は確率変数の値の和をとっているだけなので、変数の値が全てn倍されたら期待値もn倍されます。

E[X+Y] = E[X] + E[Y]

二つの確率変数 X, Y があったとき、和の期待値は、期待値の和に等しいという性質は、確率変数が互いに独立でなくても成立します。期待値の定義を考えると確率の足し算をしているだけですから、和について「くくりだし」が可能です。

確率変数という言葉がわかりにくい場合は、サイコロを考えてください。二つのサイコロの目を足した数の期待値（平均）は、個々のサイコロの期待値（平均）の和ということです。例えば、サイコロ2個を振って出る目を足した数の平均値を数え上げて求めるのは、目の組み合わせが1,1の場合から6,6の場合まで数え上げなくてはならず大変です。 しかし、上の式を用いれば簡単に求められます。

例. サイコロ2個の和の期待値
E[サイコロ2個の和] = E[サイコロ1個] + E[サイコロ1個] = 3.5 + 3.5 = 7
E[コイン10枚で表が出る] = 10 * E[コイン1枚] = 10 * 1/2 = 5

では、サイコロの目を足すかわりに掛けた場合、目の期待値を簡単に求められるでしょうか。 二つのサイコロが独立のときに限り、期待値は積についても分配できます。

例. サイコロ2個の積の期待値
E[サイコロ2個の積] = ( E[サイコロ1個] )2 = (3.5)2 = 12.25
E[コイン2枚の積] = ( E[コイン1枚] )2 = (1/2)2 = 0.25

コイン2枚のほうは、両方とも表が出ないと積が1になりません。期待値0.25という結果は納得がいきます。

分散

確率変数（例えばサイコロ）がとる値のばらつきの度合いを分散といいます。　分散は英語でVarianceなので V[確率変数] と書きます。

定義
V[X] = E[(X-E[X])2] = E[X2] -(E[X])2

二つ目の等式は以下のようにして成立します。

\textstyle \begin{alignat}{2} V[E] &= E[(X-E[X])^2]\\ &= E[X^2 -2E[X] * X + E[X]^2]\\ &= E[X^2] - E[ 2E[X] * X] + E[X]^2\\ &= E[X^2] - 2E[X]E[X] + E[X]^2\\ &= E[X^2] - E[X]^2 \end{alignat}

例.　フェアなサイコロの分散
V[サイコロ] = 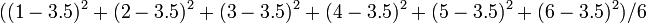((1-3.5)^2+(2-3.5)^2+(3-3.5)^2+(4-3.5)^2+(5-3.5)^2+(6-3.5)^2)/6 = 35/12 (≒ 2.916)
V[n X] = n2 V[X] (n ... 実数)
証明
\begin{alignat}{2} V[nX] &= E[(nX)^2] - E[nX]^2\\ &= n^2E[X^2] - n^2E[X]^2\\ &= n^2 V[X] \end{alignat}
例.　サイコロの目の2倍の分散
サイコロの目の2倍は、2個のサイコロの目を足したものとは違うことに注意しましょう。目を2倍しても、例えば奇数の値は決して出てきません。
V[2*サイコロ] = 4 * 35 / 12 = 35 / 3
V[X+Y] = V[X] + V[Y] (ただし X,Y は独立)

X,Y が独立であれば、和の分散は分散の和に等しくなります。しかし独立でない場合には V[X+Y] > V[X] + V[Y] です。この「ズレ」部分を共分散 (covariance) と呼びます。

V[X+Y] = V[X] + V[Y] + 2Cov[X,Y]
例　2個のサイコロの目の和の分散
V[サイコロ+サイコロ] = 35/12 + 35/12 = 35/6

サイコロを1個振ってその目を二倍した場合、2から12までの偶数が等確率(1/6)で出てきます。しかし2個のサイコロの和の場合、同じく2から12までの数が出てきますが、2や12はそれぞれ1/36の確率です。6は(1,5) (2,4) (3,3) (4,2) (5,1)という組み合わせがありうるので5/36の確率で出てきます。つまり、6や7という平均的な値が出やすくなっているので、目の二倍よりも分散が小さくなります。

例 複数のサイコロの目の平均の分散

ここで応用例として、n 個のサイコロを振ったときの、目の平均値の分散を考えてみましょう。個々のサイコロの目の期待値は7/2です。n 個の平均の期待値は7/2のまま変わりません。しかし分散は違います。n 個のサイコロの目の和の分散を計算してみましょう。ここではサイコロを X と記述します。

V[(X1+X2+ ... Xn)/n]
= (1/n2)V[X1+X2+ ... Xn]
= (1/n2)n V[X]
= (1/n)V[X] = 35/12n

サイコロの数が多ければ多いほど、分散は0に近づくことがわかります。たくさん投げるほど平均値は7/2に近づきますから、納得のいく結果になりました。

共分散

共分散 (covariance) は二組の対応する確率変数の間で、ばらつきが異なる度合いです。数式にすると、Xにおいて平均からズレた量とYにおいて平均からズレた量を掛け算して平均したものにあたります。

定義
Cov[X,Y]=E[(X-E[X])(Y-E[Y])] = E[XY] - E[X]E[Y]

等式の二つ目は、分散の定義における証明と同じ理由で成立します。 この定義から

Cov[X,Y] = Cov[Y,X]
Cov[X,X] = V[X]

です。共分散はXとYに関して対称に定義されていて、XとYが独立なら0になります。 XとYのばらつきの傾向が似ていれば大きな正の値になり、似ていなければ大きな負の値になります。

共分散という定義が概念的に捉えにくい場合、相関という概念を考えると良いでしょう。

相関

共分散をXの標準偏差とYの標準偏差で割ったものが相関係数です。

Corr[X,Y] = Cov[X,Y] /(V[X]^{1/2}V[Y]^{1/2})
Retrieved from "http://metabolomics.jp/mediawiki/index.php?title=Aritalab:Lecture/Basic/Expectation&oldid=254438"
Personal tools
Namespaces

Variants
Actions
Navigation
metabolites
Toolbox