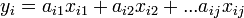Revision as of 14:23, 19 May 2011

確率

よく見る釣鐘型の分布。どんな分布でも、その中から要素をランダムに抽出して和をとったものの分布は、正規分布に近づく（中心極限定理）。期待値が0, 分散が1になるようにスケーリングしたものを標準正規分布といい、 $N(0,1)$ と書く。

標準正規分布表の見方。

表におけるzの値は上から順に左→右方向にみる。正規分布全体の面積を1.0としたときの、 zから上側の面積を示している。例えば標準偏差が2.0以上の面積は0.0228、2.2以上の面積は0.0139。

稀にしか起こらない離散的な事象を数える際に用いる分布。単位時間中に平均λ回発生する事象が、ぴったりk回発生する確率を

$P(N=k) = \frac{e^{-\lambda}\lambda^k}{k!}$

と定義する。

コイン投げをして表裏がでる回数を記録したときにできる分布。離散的な分布だが、フェアなコインを30回程度投げると正規分布で非常によく近似できる。

母集団から無作為に抽出された標本集団から、もとの母集団を統計的に推し量ることを推定という。

従属変数（近似したい値、目的変数ともいう）と説明変数（近似に用いるデータ）の関係を統計的に推定することを回帰分析という。１個の説明変数から１個の従属変数を予測する場合を単回帰、説明変数を複数用いる場合を重回帰という。従属変数をy、説明変数をxとすると

$y_i = a_{i1}x_{i1} + a_{i2}x_{i2} + ... a_{ij}x_{ij}$

の形でパラメータa_{ij}を最小二乗法で決定する線形回帰が一般的。

標本の値から、母集団の平均値や分散を予測することを点推定（数値を点として予測）と呼び、その推定がどれ位ずれているかを区間推定と呼ぶ。

@@ Line 1: / Line 1: @@
 =確率=
-* [[Aritalab:Lecture/Basic/Expectation|期待値・平均について]]
+* [[Aritalab:Lecture/Basic/Expectation|期待値と分散について]]
-* [[Aritalab:Lecture/Basic/Variance|分散・共分散について]]
-===ベイズ推定===
-ベイズの定理は以下のように表される。
-:<math>P(A|B) = P(B|A)P(A)/P(B)</math>
-ここでP(A)を事前確率、P(A|B)を（Bが起きることを知った上でのAが起きる確率という意味の）事後確率と呼ぶ。
-<!---
-参考 [http://ja.wikipedia.org/wiki/%E3%83%A2%E3%83%B3%E3%83%86%E3%82%A3%E3%83%BB%E3%83%9B%E3%83%BC%E3%83%AB%E5%95%8F%E9%A1%8C モンティ・ホール問題]
-:3つの扉のうち1つだけに賞品が入っている。ただし扉は次のように2段階で選べる。
-まず回答者は3つの扉からどれか1つを選ぶ。
-次に、答を知っている司会者が、選んでいない扉で賞品の入っていない扉1つを開けてみせる。ただし、回答者が当たりの扉を選んでいる場合は、残りの扉からランダムに1つを選んで開けるとする。このあと回答者は扉を1回選び直してもよい。
-で扉を換えるのと換えないのと、どちらが当る確率が高いか？
---->
 =分布=
 ==正規分布==