Aritalab:Lecture/NetworkBiology/Link Analysis
From Metabolomics.JP
< Aritalab:Lecture | NetworkBiology(Difference between revisions)
| Line 2: | Line 2: | ||
==Centrality== | ==Centrality== | ||
| − | + | 無向グラフにおいて、頂点のネットワーク中心への近さを示す尺度を中心度(centrality)という。いずれの値も0-1の間をとるように正規化する。有向グラフでも定義できるが、次に述べるprestigeを使った方がよい。 | |
| − | * Degree centrality ... | + | * Degree centrality ... 辺数が多い点を中心と考える。 |
| − | * Closeness centrality ... | + | * Closeness centrality ... 全頂点への平均最短距離が短い点を中心と考える。 |
| − | * Betweenness centrality ... | + | * Betweenness centrality ... 全頂点間の最短経路に多く使われる点を中心と考える。同じ値で辺のbetweennessも定義できる。 |
{| | {| | ||
| Line 19: | Line 19: | ||
|Closeness | |Closeness | ||
|colspan="2"| <math>C_C(i)=\frac{n-1}{\sigma^n_{j=1}d(i,j)}</math> | |colspan="2"| <math>C_C(i)=\frac{n-1}{\sigma^n_{j=1}d(i,j)}</math> | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
|Betweenness | |Betweenness | ||
| − | | <math>C_B(i)=\sigma_{j<k}\frac{p_{jk}(i)}{p_{jk}} \times N_{paths}^{-1}</math> | + | |colspan="2"| <math>C_B(i)=\sigma_{j<k}\frac{p_{jk}(i)}{p_{jk}} \times N_{paths}^{-1}</math><br> |
| − | + | <small> | |
| − | + | ||
| − | + | ||
ただしj,kはiと異なる頂点。iを除いた最短経路の本数は無向で<math>\frac{(n-1)(n-2)}{2}</math>、有向で<math>(n-1)(n-2)</math>。 | ただしj,kはiと異なる頂点。iを除いた最短経路の本数は無向で<math>\frac{(n-1)(n-2)}{2}</math>、有向で<math>(n-1)(n-2)</math>。 | ||
</small> | </small> | ||
| Line 33: | Line 28: | ||
==Prestige== | ==Prestige== | ||
| + | 有向グラフにおいて頂点の傑出具合を測る尺度を傑出度(prestige)という。 | ||
| + | * Degree prestige ... 多くの入力辺がある点を傑出していると | ||
| + | 考える。 | ||
| + | * Proximity prestige ... より多くの頂点から到達できる点を傑出していると考える。Degree prestigeの拡張になっている。 | ||
| + | * Rank prestige ... 高いランクの頂点に指されている頂点もランクが高いと考える。 | ||
| + | |||
| + | {| | ||
| + | ! Name || | ||
| + | |- | ||
| + | | Degree || <math>P_D(i)=\frac{d_{in}(i)}{n-1}</math> | ||
| + | |- | ||
| + | | Proximity || <math>P_P(i)=\frac{|I_i|/(n-1)}{\sum_{j\in I_i}d(j,i)/|I_i|}</math><br> | ||
| + | <small><math>I_i</math>は''i''より到達できる頂点集合</small> | ||
| + | |- | ||
| + | | Rank || <math>\mathbf{P_R=A^TP_R}</math><br> | ||
| + | <small><math>\mathbf{P_R}</math>は長さ''n''の縦ベクトル、<math>\mathbf{A}</math>は隣接行列。つまり<math>\mathbf{P_R}</math>は<math>\mathbf{A}</math>の固有値。</small> | ||
| + | |} | ||
| + | |||
| + | |||
| + | |} | ||
Revision as of 22:13, 22 April 2009
歴史
Centrality
無向グラフにおいて、頂点のネットワーク中心への近さを示す尺度を中心度(centrality)という。いずれの値も0-1の間をとるように正規化する。有向グラフでも定義できるが、次に述べるprestigeを使った方がよい。
- Degree centrality ... 辺数が多い点を中心と考える。
- Closeness centrality ... 全頂点への平均最短距離が短い点を中心と考える。
- Betweenness centrality ... 全頂点間の最短経路に多く使われる点を中心と考える。同じ値で辺のbetweennessも定義できる。
| Name | Undirected | Directed |
|---|---|---|
| Degree | 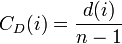 |
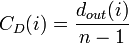
|
|
| ||
| Closeness | 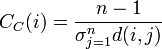
| |
| Betweenness | 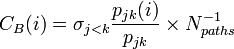
ただしj,kはiと異なる頂点。iを除いた最短経路の本数は無向で | |
Prestige
有向グラフにおいて頂点の傑出具合を測る尺度を傑出度(prestige)という。
- Degree prestige ... 多くの入力辺がある点を傑出していると
考える。
- Proximity prestige ... より多くの頂点から到達できる点を傑出していると考える。Degree prestigeの拡張になっている。
- Rank prestige ... 高いランクの頂点に指されている頂点もランクが高いと考える。
| Name | |
|---|---|
| Degree | 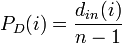
|
| Proximity | 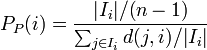
|
| Rank | 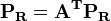
|
|}
 、有向で
、有向で 。
。
 はiより到達できる頂点集合
はiより到達できる頂点集合
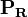 は長さnの縦ベクトル、
は長さnの縦ベクトル、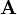 は隣接行列。つまり
は隣接行列。つまり