Aritalab:Lecture/Basic/Probability

確率の基礎

確率の定義

確率を論じるためには

1. 起こりうるすべての事象を含む標本空間 Ω
2. 実際に起こりうる事象の集合 F
3. 各事象が起こる確率を与える関数 Pr: F → R

が必要です。ここで使う関数のことを一般に確率測度とよびます。確率測度は

1. Pr(Ω) = 1
2. どの事象 E についても 0 ≤ Pr(E) ≤ 1
3. 加算個の独立な事象について $\mbox{Pr}\Big(\cup_{i\geq 1} E_i\Big) = \sum_{i \geq 1} \mbox{Pr} (E_i)$

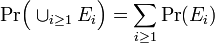
を満たさなくてはならず、コルモゴロフの公理と呼ばれています。Pr(E) を事象 E の確率と呼びます。

条件付き確率

事象 F が起こったあとで事象 E が起きる条件付き確率を

Pr( E | F ) = Pr( E ∩ F) / Pr (F)

と書きます。F が起こる確率の内訳としての Pr( E ∩ F) を求めるわけです。もし E と F が独立の事象なら Pr( E | F ) = Pr (E) になります。

全確率の法則

任意の確率は、互いに背反な事象 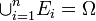$\cup^n_{i=1}E_i = \Omega$ を用いて

$\mbox{Pr}(B) = \sum^n_{i=1}\mbox{Pr}(B|E_i)\mbox{Pr}(E_i)$

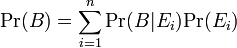
と書けます。

ベイズの法則

互いに背反な事象 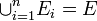$\cup^n_{i=1}E_i = E$ にたいして

$\mbox{Pr}(E_i|B) = \frac{\mbox{Pr}(E_i \cap B)}{\mbox{Pr}(B)} = \frac{\mbox{Pr}(E_i \cap B)}{\sum^n_{i=1}\mbox{Pr}(B|E_i)\mbox{Pr}(E_i)} = \frac{\mbox{Pr}(B | E_i)\mbox{Pr}(E_i)}{\sum^n_{i=1}\mbox{Pr}(B|E_i)\mbox{Pr}(E_i)}$

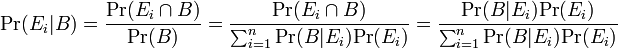
事象 E_i に対して Pr(E_i) は事象 B が起こる前に与えられる確率であるから事前確率といい、Pr( E_i| B ) は B が起こった後で与えられる確率であるから事後確率といいます。

例

いかさまコインを見分ける

3枚のコインがあり、そのうち1枚だけは表が2/3、残りは1/2の確率で出るとします。i 番目のコインがいかさまである事象を E_i と書きましょう。最初は Pr (E_i) = 1/3 ( i = 1,2,3) です。

いま、3枚のコインを順に投げて 表　裏　裏　が出たとします。この事象を B と書き、E_i に対する条件付き確率を求めてみます。

Pr(B | E₁) = 2/3 × 1/2 × 1/2 = 1/6

Pr(B | E₂) = 1/2 × 1/3 × 1/2 = 1/12

Pr(B | E₃) = 1/2 × 1/2 × 1/3 = 1/12

Pr(B) = Σ_i³ Pr(B | E_i) Pr(E_i) = 1/6 * 1/3 + 1/12 * 1/3 + 1/12 * 1/3 = 1/9

ベイズの法則を用いると

Pr(E₁|B) = Pr(B | E₁) Pr(E₁) / Pr(B) = 1/6 * 1/3 * 9 = 1/2

です。つまり、3枚のコインをフリップして 表　裏　裏　と出るのを見たことにより、1枚目のコインがいかさまである確率が 1/3 から 1/2 に上がりました。