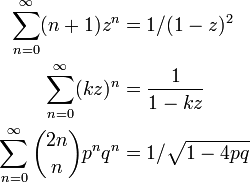Aritalab:Lecture/Basic/Generating Function
From Metabolomics.JP
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
母関数
扱う対象とする無限列を、補助変数 z を用いてべき級数 (power series) として表現する方法を母関数 (generating function) といいます。
母関数の例
ここでは以下の3つの公式を、母関数を用いて導きます。
|
|
自然数
an = n + 1 の母関数は

です。この右辺を閉じた式にするには
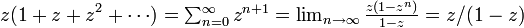
を使います。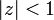 で収束すると仮定し、両辺を z について微分します。
で収束すると仮定し、両辺を z について微分します。
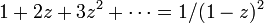
少し拡張してみましょう。
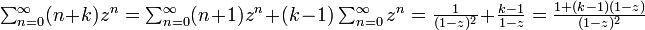
べき乗
an = 2n の母関数は
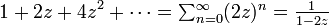
です。ただし 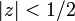 と仮定します。一般化すれば an = kn の母関数が 1/(1 − kz) になります。
と仮定します。一般化すれば an = kn の母関数が 1/(1 − kz) になります。
二項定理
二項定理は、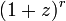 が数列
が数列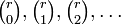 の母関数表現と解釈できます。すなわち
の母関数表現と解釈できます。すなわち

が成立します。この式を二つ掛け合わせると
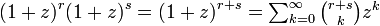
両者の Σ 式において zn の係数が等しいとおけば
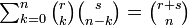
が得られます。これをヴァンデルモンドの畳み込み式 (convolution) といいます。 一般化すると以下のように書けます。
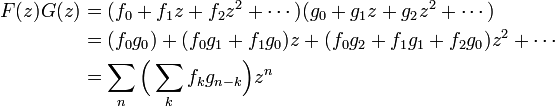
- 二項定理の応用
数列 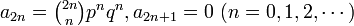 の母関数が
の母関数が 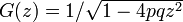 になることを示しましょう。この式はランダムウォークの解析で出てきます。
になることを示しましょう。この式はランダムウォークの解析で出てきます。
まず数列の定義から
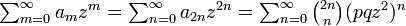
です。次に

と、二項定理 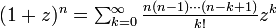 を用いて
を用いて
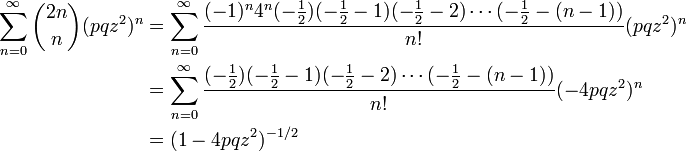
を示せました。この母関数で z = 1 とおくと  になります。
になります。