Aritalab:Lecture/NetworkBiology/Markov Chains/Coupling
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
確率分布の距離
二つの確率分布 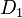 と
と  の距離を次のように定義する。
の距離を次のように定義する。
- [定義] 変動距離
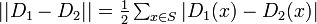
右辺の係数 1/2 は 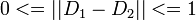 を満たすためについており、
を満たすためについており、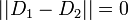 なら全要素について分布が等しいから
なら全要素について分布が等しいから 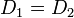 である。また距離が 1 のときは確率が正となる状態の集合が独立であることを意味している。
変動距離は、特定の事象に対する確率の差を用いても定義できる。
である。また距離が 1 のときは確率が正となる状態の集合が独立であることを意味している。
変動距離は、特定の事象に対する確率の差を用いても定義できる。
- 定理
任意の 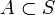 において
において 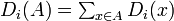 とする。このとき
とする。このとき
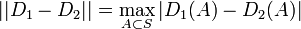
- 証明
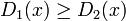 を満たす状態の集合を
を満たす状態の集合を 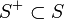 、
、
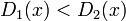 を満たす状態の集合を
を満たす状態の集合を 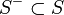 と書く。
このとき
と書く。
このとき
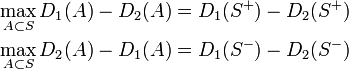
また
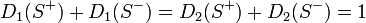
より
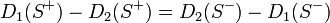
したがって
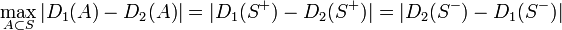
最後に
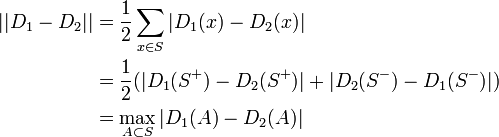
カップリング
状態空間 S 上のマルコフ連鎖 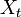 ,
, 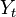 がカップリング (coupling) するとは、時刻 t 以降に二つの確率過程が同じ状態を取ること、つまり
がカップリング (coupling) するとは、時刻 t 以降に二つの確率過程が同じ状態を取ること、つまり 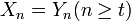 をいう。この時刻 t をカップリング時間という。
をいう。この時刻 t をカップリング時間という。
ただひとつの定常分布を持つ規約でエルゴード的なマルコフ連鎖の場合、任意の初期分布と定数  に対して、ある数 T が存在し、 T ステップ後に定常分布との間の変動距離を
に対して、ある数 T が存在し、 T ステップ後に定常分布との間の変動距離を  以下にすることができる。
以下にすることができる。
定常分布を表す 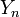 と、任意の状態集合
と、任意の状態集合 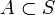 において
において
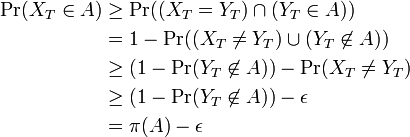
同じ議論を補集合 S-A に適用すると 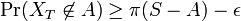 。
すなわち
。
すなわち  であるため、時刻 T 以降に定常分布へ収束することがわかる。
であるため、時刻 T 以降に定常分布へ収束することがわかる。
具体例
- トランプのシャッフル
二組のトランプを用意し、一組目 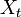 は52枚のカードから等確率で一枚選び、一番上におく。
もう一組
は52枚のカードから等確率で一枚選び、一番上におく。
もう一組 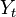 のほうは、X で選んだ値を同様に一番上におく。
のほうは、X で選んだ値を同様に一番上におく。
選ばれて一度上に移動したカードの位置は、 X と Y の間で変わらない。
そのため、全てのカードが少なくとも一度選ばれた時点でカップリングが起こり、その後の動作が全て同一になる。
全てのカードが少なくとも1回選ばれるのに必要な回数の期待値は 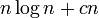 と書ける (cは定数)。
いずれか一枚のカードがまだ選ばれていない確率は
と書ける (cは定数)。
いずれか一枚のカードがまだ選ばれていない確率は
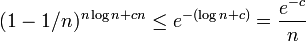
したがって n 枚のうちどれかが一つでも選ばれていない確率は高々 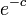 。
例えば、
。
例えば、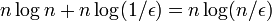 回シャッフルした後は、カップリングしていない確率は高々
回シャッフルした後は、カップリングしていない確率は高々  になる。
になる。