Aritalab:Lecture/Biochem/Modularity
(Created page with "==バイオロジーとモジュール== ;From molecular to modular cell biology : Hartwell LH, Hopfield JJ, Leibler S, Murray AW in ''Nature'' 402(6761 Suppl):C47-52 * Hodgkin...") |
m (→バイオロジーとモジュール) |
||
| (6 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
==バイオロジーとモジュール== | ==バイオロジーとモジュール== | ||
| + | システム生物学においては、複雑なメカニズムを解析するのにコンポーネントへの分解が必須と考えられています。 | ||
| + | これはモジュラー生物学として提唱されてはいますが、まだ大きなブレイクスルーはありません。 | ||
;From molecular to modular cell biology | ;From molecular to modular cell biology | ||
: Hartwell LH, Hopfield JJ, Leibler S, Murray AW in ''Nature'' 402(6761 Suppl):C47-52 | : Hartwell LH, Hopfield JJ, Leibler S, Murray AW in ''Nature'' 402(6761 Suppl):C47-52 | ||
| − | |||
| − | |||
| + | <!---- | ||
| + | ==Hodgkin–Huxley 方程式== | ||
| + | Journal of Physiology 117(1952)500においてニューロンのスパイクをモデル化した4変数の非線形微分方程式です。 | ||
| + | ---> | ||
==フィードバックループ== | ==フィードバックループ== | ||
| − | + | <center> | |
| − | + | "The constancy of the internal environment is the condition for a free and independent life" ---Claude Bernard--- | |
| − | + | </center> | |
| − | + | ||
| − | + | ||
| − | + | フィードバックは生体内の代表的なモジュールで、特に遺伝子発現や代謝のホメオスタシスを保つのに必要です。 | |
| − | + | 入力信号を高めるように働く効果を正、弱めるように働く場合を負といいます。 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ===負のフィードバック=== | |
| − | [[File:Lecture-Biochem-Modularity- | + | [[File:Lecture-Biochem-Modularity-nf.png|Negative Feedback|60px|thumb]] |
| − | |} | + | 負のフィードバックは出力量に比例して入力部分を抑えるように働くため、以下の効果を持ちます。 |
| + | * 平衡状態に導いて安定させる | ||
| + | * 振動させる | ||
| + | 安定効果は想像しやすいですが、振動現象はわかりにくいかもしれません。 | ||
| + | シミュレーションソフトを用いると、その動きを実感することができます。（[[Aritalab:Lecture/Biochem/Modularity/NF|Cell Designerによるシミュレーションページへ]]） | ||
| + | |||
| + | |||
| + | ===正のフィードバック=== | ||
| + | [[File:Lecture-Biochem-Modularity-pf.png|Positive Feedback|60px|thumb]] | ||
| + | 正のフィードバックは入力を増強させるように働くため、出力を 0 か 1 かといった極端な値に固定する働き（スイッチ効果）を持ちます。この現象をヒステリシスとも呼びます。その挙動はHill式<math>\textstyle \theta = \frac{x^L}{K + x^L} </math>であらわされます。''L''の値が大きいほどスイッチ効果が高く、この項は協調性 (cooperativity) やアロステリー (allostery) で説明されます。 | ||
| + | |||
| + | |||
| + | ===バイスタビリティ=== | ||
| + | [[File:Lecture-Biochem-Modularity-bs.png|Bistability|60px|thumb]] | ||
| + | 細胞周期や分化のように二つ以上の安定状態を持つ場合を双安定とよびます。正のフィードバックと負のフィードバックを併せ持つことで実現できます。 | ||
| + | |||
| + | |||
| + | |||
| + | ==フィードフォワードループ== | ||
| + | 2000年を過ぎて急に注目され始めたモジュールが、フィードフォワードループです。とりわけ Uri Alon のグループが解析する大腸菌の転写因子に関するモデルが有名です。 | ||
| + | |||
| + | 大腸菌は周りの環境を数秒間で感知し、数分のうちに必要なタンパク質の合成を開始します。このような迅速な対応は、フィードバックループでは難しいと考えられています。大腸菌には転写制御因子が400ほどあり、これらが遺伝子とどのような相互作用をするのか、詳細なネットワーク解析がなされました。 | ||
| + | * R Milo, S Shen-Orr, S Itzkovitz, N Kashtan, D Chklovskii, U Alon )2002) "Network Motifs: Simple Building Blocks of Complex Networks" Science, 298:824-827 | ||
| + | * U Alon (2007) "Network motifs: theory and experimental approaches" Nature Reviews Genetics 8, 450-461 | ||
| + | ===ネットワークモチーフ=== | ||
{| | {| | ||
|valign="top"| | |valign="top"| | ||
| − | + | 転写制御ネットワークの中に、ランダムなネットワークと比較して頻出するパターンをネットワークモチーフと呼びます。 | |
| − | + | ||
| − | + | たとえば大腸菌の転写制御因子のおよそ1割は自分自身を制御するフィードバックループを持っています。フィードバックはタンパク質の産生量を安定化させるのに必要なモチーフというわけです。さらに、3つの遺伝子間の制御関係を調べてみると、考えられる13のパターンの中で、フィードフォワードループ (FFL) といわれる形が最も多い（40個程度ある)ことがわかりました。それに対して、3頂点のフィードバックループは大腸菌の転写制御因子には1つもありません。<br/> | |
| − | [[File:Lecture-Biochem-Modularity- | + | [[File:Lecture-Biochem-Modularity-FFL.png]] |
| − | + | ||
| − | + | FFLには、負の制御と正の制御を考えれば 2<sup>3</sup> = 8 通りの制御関係が考えられます。そのうち、論理的につじつまがあう制御関係は半分です。 | |
| − | + | 大腸菌と酵母の転写制御因子を調べると、8 通りの制御関係のうち 2 通りだけが頻出することがわかりました。 | |
| − | + | コヒーレントなフィードフォワードループは on/off 感受性を遅らせる '''ノイズ除去フィルター''' としてはたらくことがわかっています。 | |
| − | + | アラビノースの制御系で用いられていることがわかりました。グルコースが無く、アラビノースだけが存在する状況で必要な遺伝子を産生する際に利用されます。 | |
| − | [[File:Lecture-Biochem-Modularity- | + | またインコヒーレントなフィードフォワードループは '''パルス生成器''' として働きます。応答時間を加速しているのです。 |
| + | | | ||
| + | [[File:Lecture-Biochem-Modularity-FFL2.jpg|400px]] | ||
|} | |} | ||
Latest revision as of 09:27, 7 July 2011
Contents |
[edit] バイオロジーとモジュール
システム生物学においては、複雑なメカニズムを解析するのにコンポーネントへの分解が必須と考えられています。 これはモジュラー生物学として提唱されてはいますが、まだ大きなブレイクスルーはありません。
- From molecular to modular cell biology
- Hartwell LH, Hopfield JJ, Leibler S, Murray AW in Nature 402(6761 Suppl):C47-52
[edit] フィードバックループ
"The constancy of the internal environment is the condition for a free and independent life" ---Claude Bernard---
フィードバックは生体内の代表的なモジュールで、特に遺伝子発現や代謝のホメオスタシスを保つのに必要です。 入力信号を高めるように働く効果を正、弱めるように働く場合を負といいます。
[edit] 負のフィードバック
負のフィードバックは出力量に比例して入力部分を抑えるように働くため、以下の効果を持ちます。
- 平衡状態に導いて安定させる
- 振動させる
安定効果は想像しやすいですが、振動現象はわかりにくいかもしれません。 シミュレーションソフトを用いると、その動きを実感することができます。（Cell Designerによるシミュレーションページへ）
[edit] 正のフィードバック
正のフィードバックは入力を増強させるように働くため、出力を 0 か 1 かといった極端な値に固定する働き（スイッチ効果）を持ちます。この現象をヒステリシスとも呼びます。その挙動はHill式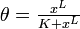
であらわされます。Lの値が大きいほどスイッチ効果が高く、この項は協調性 (cooperativity) やアロステリー (allostery) で説明されます。
[edit] バイスタビリティ
細胞周期や分化のように二つ以上の安定状態を持つ場合を双安定とよびます。正のフィードバックと負のフィードバックを併せ持つことで実現できます。
[edit] フィードフォワードループ
2000年を過ぎて急に注目され始めたモジュールが、フィードフォワードループです。とりわけ Uri Alon のグループが解析する大腸菌の転写因子に関するモデルが有名です。
大腸菌は周りの環境を数秒間で感知し、数分のうちに必要なタンパク質の合成を開始します。このような迅速な対応は、フィードバックループでは難しいと考えられています。大腸菌には転写制御因子が400ほどあり、これらが遺伝子とどのような相互作用をするのか、詳細なネットワーク解析がなされました。
- R Milo, S Shen-Orr, S Itzkovitz, N Kashtan, D Chklovskii, U Alon )2002) "Network Motifs: Simple Building Blocks of Complex Networks" Science, 298:824-827
- U Alon (2007) "Network motifs: theory and experimental approaches" Nature Reviews Genetics 8, 450-461
[edit] ネットワークモチーフ
|
転写制御ネットワークの中に、ランダムなネットワークと比較して頻出するパターンをネットワークモチーフと呼びます。 たとえば大腸菌の転写制御因子のおよそ1割は自分自身を制御するフィードバックループを持っています。フィードバックはタンパク質の産生量を安定化させるのに必要なモチーフというわけです。さらに、3つの遺伝子間の制御関係を調べてみると、考えられる13のパターンの中で、フィードフォワードループ (FFL) といわれる形が最も多い（40個程度ある)ことがわかりました。それに対して、3頂点のフィードバックループは大腸菌の転写制御因子には1つもありません。 FFLには、負の制御と正の制御を考えれば 23 = 8 通りの制御関係が考えられます。そのうち、論理的につじつまがあう制御関係は半分です。 大腸菌と酵母の転写制御因子を調べると、8 通りの制御関係のうち 2 通りだけが頻出することがわかりました。 コヒーレントなフィードフォワードループは on/off 感受性を遅らせる ノイズ除去フィルター としてはたらくことがわかっています。 アラビノースの制御系で用いられていることがわかりました。グルコースが無く、アラビノースだけが存在する状況で必要な遺伝子を産生する際に利用されます。 またインコヒーレントなフィードフォワードループは パルス生成器 として働きます。応答時間を加速しているのです。 |
|
