Aritalab:Lecture/NetworkBiology/Watts-Strogatz Model
From Metabolomics.JP
< Aritalab:Lecture | NetworkBiology(Difference between revisions)
| Line 1: | Line 1: | ||
| − | =歴史と参考図書= | + | ==歴史と参考図書== |
* Watts DJ, Strogatz SH. "Collective dynamics of 'small-world' networks.". Nature 393 (6684):409–10, 1998. [http://www.ncbi.nlm.nih.gov/sites/entrez?db=pubmed&uid=9623998&cmd=showdetailview&indexed=google doi:10.1038/30918] | * Watts DJ, Strogatz SH. "Collective dynamics of 'small-world' networks.". Nature 393 (6684):409–10, 1998. [http://www.ncbi.nlm.nih.gov/sites/entrez?db=pubmed&uid=9623998&cmd=showdetailview&indexed=google doi:10.1038/30918] | ||
* Durrett R. "Random Graph Dynamics" Cambridge University Press, 2004. | * Durrett R. "Random Graph Dynamics" Cambridge University Press, 2004. | ||
| − | =Watts-Strogatz Model= | + | ==Watts-Strogatz Model= |
各頂点が<math>k</math>個の隣接点に接続した環状の格子グラフにおいて（総辺数は<math>kn/2</math>）、確率<math>p</math>で辺を張り直したものをWatts-Strogatzモデルという。辺を張りなおすモデルは解析が難しいので、環状の格子グラフにポアソン過程として<math>pkn/2</math>本の辺を追加するモデルがよく使われる。パラメータ<math>p</math>を調節して格子とランダムグラフの中間状態を作成する点がポイント。 | 各頂点が<math>k</math>個の隣接点に接続した環状の格子グラフにおいて（総辺数は<math>kn/2</math>）、確率<math>p</math>で辺を張り直したものをWatts-Strogatzモデルという。辺を張りなおすモデルは解析が難しいので、環状の格子グラフにポアソン過程として<math>pkn/2</math>本の辺を追加するモデルがよく使われる。パラメータ<math>p</math>を調節して格子とランダムグラフの中間状態を作成する点がポイント。 | ||
| − | ==<math>p=0</math>のとき== | + | ===<math>p=0</math>のとき=== |
;クラスター係数 | ;クラスター係数 | ||
簡単のため左右の隣接点に同じ本数リンクを張ると仮定し、<math>k = 2i</math>とする。注目する点を原点とした<math>-i \leq x, y < \leq i</math>のxy座標系を考えたとき、<math>|x - y| > i</math>に対応する座標点は三角形<math>K_3</math>を形成せず、残りは形成する。その割合を考えると<math>C(0) = 3/4</math>。 | 簡単のため左右の隣接点に同じ本数リンクを張ると仮定し、<math>k = 2i</math>とする。注目する点を原点とした<math>-i \leq x, y < \leq i</math>のxy座標系を考えたとき、<math>|x - y| > i</math>に対応する座標点は三角形<math>K_3</math>を形成せず、残りは形成する。その割合を考えると<math>C(0) = 3/4</math>。 | ||
;平均頂点間距離 | ;平均頂点間距離 | ||
1ステップで<math>k/2</math>点スキップでき、環状格子で一番離れている点は<math>n/2</math>なので、<math>L(0) \leq n / k</math>。 | 1ステップで<math>k/2</math>点スキップでき、環状格子で一番離れている点は<math>n/2</math>なので、<math>L(0) \leq n / k</math>。 | ||
| − | ==<math>p=1</math>のとき== | + | ===<math>p=1</math>のとき=== |
ランダムグラフと思えばよい。 | ランダムグラフと思えばよい。 | ||
;クラスター係数 | ;クラスター係数 | ||
| Line 18: | Line 18: | ||
辺をランダムに張りかえるので<math>L(1) \simeq \log n / \log k</math>。 | 辺をランダムに張りかえるので<math>L(1) \simeq \log n / \log k</math>。 | ||
| − | ==一般の場合== | + | ===一般の場合=== |
;平均頂点間距離 | ;平均頂点間距離 | ||
導出は面倒だが以下の近似が知られている。<math>\textstyle L(p)=\frac{n}{k}\frac{\log(2 pkn)}{4 pkn}</math> | 導出は面倒だが以下の近似が知られている。<math>\textstyle L(p)=\frac{n}{k}\frac{\log(2 pkn)}{4 pkn}</math> | ||
Revision as of 14:02, 2 June 2010
Contents |
歴史と参考図書
- Watts DJ, Strogatz SH. "Collective dynamics of 'small-world' networks.". Nature 393 (6684):409–10, 1998. doi:10.1038/30918
- Durrett R. "Random Graph Dynamics" Cambridge University Press, 2004.
=Watts-Strogatz Model
各頂点が
個の隣接点に接続した環状の格子グラフにおいて（総辺数は
）、確率
で辺を張り直したものをWatts-Strogatzモデルという。辺を張りなおすモデルは解析が難しいので、環状の格子グラフにポアソン過程として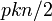
本の辺を追加するモデルがよく使われる。パラメータを調節して格子とランダムグラフの中間状態を作成する点がポイント。
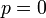のとき
- クラスター係数
簡単のため左右の隣接点に同じ本数リンクを張ると仮定し、
とする。注目する点を原点とした
のxy座標系を考えたとき、
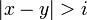に対応する座標点は三角形
を形成せず、残りは形成する。その割合を考えると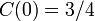
。
- 平均頂点間距離
1ステップで
点スキップでき、環状格子で一番離れている点は
なので、
。
のとき
ランダムグラフと思えばよい。
- クラスター係数
辺を張りかえるとき、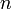
頂点の中から隣接点を選べばよいので
。
- 平均頂点間距離
辺をランダムに張りかえるので
。
一般の場合
- 平均頂点間距離
導出は面倒だが以下の近似が知られている。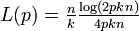
- クラスター係数
簡単な近似では、をなす3頂点間の辺が張りなおしを防げばよいので
。
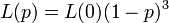