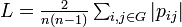Aritalab:Lecture/NetworkBiology/CC APL

ネットワークの指標

ネットワーク全体についての尺度として、クラスター係数 C と平均頂点間距離 L を紹介します。

クラスター係数

クラスター係数は隣接する頂点間の辺の密度の平均値にあたります。まず各頂点 i におけるクラスター係数 $C_i$ を以下のように定義します。辺の長さはすべて 1 とし $(|e| = 1)$、頂点 i の次数を deg (i ), 隣接する頂点群を adj (i ) とします。

$\textstyle C_i=\frac{2}{deg(i)(deg(i)-1)} \sum_{j,k \in adj(i)} |e_{jk}|$

グラフ全体のクラスター係数はその平均値です。

$\textstyle C =\frac{1}{n} \sum^{n}_{i=1}C_i$

クラスター係数が 0.2 や 0.3 になるネットワークは、比較的「密」といえます。

平均頂点間距離

ここでは頂点 i, j 間の最短経路を 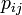$p_{ij}$ と書きます。平均頂点間距離の定義はその字のごとく全頂点間の最短路の平均値です。ネットワーク G の頂点数を n とすると頂点の組み合わせの数が n (n - 1) / 2 あるので

$\textstyle L=\frac{2}{n(n-1)} \sum_{i,j\in G}|p_{ij}|$

となります。

上の定義だと、例えば無限の広がりを持つ場合の平均距離を求められません (無限個の最短路を計算しなくてはならない)。そういう場合は、ネットワーク上のある点に注目して L を計算する場合があります。その点から距離 L 以内にある頂点数を数える手法です。

様々なグラフにおける指標の値

完全グラフ

全ての頂点間に辺を持つグラフを、完全グラフ (complete graph) といいます。完全グラフでは、 C = L = 1 になります。

木、格子

簡単のため全頂点が同じ次数を持つ木を考えましょう。中心の頂点 v₀ を根 (root) と呼びます。木はその定義よりサイクルを持たないので C = 0 です。また平均頂点間距離は、距離 L 以内にある頂点を数えることで求められます。

$\begin{align} n &= 1 + d + d(d-1) + ... + d(d-1)^L \\ &=\textstyle 1 +\frac{d (1-(d-1)^{L+1})}{(1-(d-1))} = 1 + \frac{d}{d-2}((d-1)^{L+1} -1) \\ &\propto (d-1)^{L+1} \end{align}$

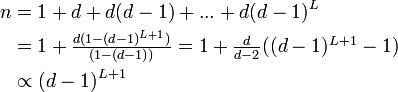
この関係から（大雑把ですが） $\textstyle L=\propto \frac{\log n}{\log (d-1)}$ となります。

格子状のネットワークでは頂点が一定間隔で配置されるため、道路網のような地理的制約をうけるつながりを表現するのに適しています。平面の場合は三角格子、正方格子、六方格子などが考えられます。ただし、クラスター係数を定義のまま適用すると、三角格子以外は隣接頂点どうしがつながらないために常に C = 0 になります。これでは面白くないので、格子の場合は最短距離が $a$ 以下の点には全て辺を張るバリエーションを考えるのが一般的です。ここでは、d 次元空間において辺の長さが単位距離の格子を Z^d と書きましょう。 ( Z^d において deg( i ) = 2 d )

Z¹ 

いわゆる数直線です。ある頂点から k の距離内にある頂点は、その数 n = 2k + 1 です。これらの頂点の平均距離は L = k になります。したがって L ∼ n/2 です。

Z² 

二次元の格子として、正方格子を考えます。ある頂点から k の距離内にある頂点の数は n = k² + ( k + 1)² です。これらの頂点の平均距離は L = k / 2 です。n の式を k について解くと $\textstyle k = \frac{\sqrt{(2n -1)} - 1}{2} \sim \frac{\sqrt{2n}}{2}$ となるため $\textstyle L \sim \frac{\sqrt{2n}}{4}$ です。

Erdős–Rényiグラフ

各頂点が持つ辺の期待値（定数）を c とします。これは c = n p を満たします。

クラスター係数 ... 辺が張られる確率は全て独立なので p です。n が大きくなると 0 に近づきます。

平均頂点間距離 ... 各頂点が持つ辺の期待値を c とします。次数 c の木構造 L ステップでグラフ全体がカバーできると考えます。 c^L = n から、L = log n / log c になります。

連結性 ... ERグラフ全体が連結であるためには、グラフ進化の考察から次数は O(log n) 以上必要です。